В геометрии прямоугольный треугольник обладает особыми свойствами, касающимися величины его углов. Рассмотрим ключевую теорему о сумме углов этой фигуры.
Содержание
Основная теорема
Сумма внутренних углов любого прямоугольного треугольника равна 180 градусам. Это частный случай общей теоремы о сумме углов треугольника в евклидовой геометрии.
Структура углов прямоугольного треугольника
| Угол | Характеристика |
| Прямой угол | Всегда равен 90° (отсюда название треугольника) |
| Острые углы (2) | Каждый меньше 90°, в сумме дают 90° |
Доказательство теоремы
- Рассмотрим прямоугольный треугольник ABC с прямым углом C
- Проведем высоту CD к гипотенузе AB
- Образовавшиеся треугольники ACD и BCD подобны исходному
- Сумма углов в каждом из них также равна 180°
- Отсюда следует, что ∠A + ∠B + ∠C = 180°
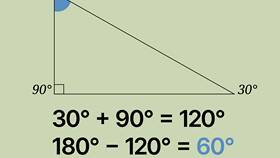
Пример расчета
Для треугольника с углами:
- Прямой угол: 90°
- Первый острый угол: 30°
- Второй острый угол: 180° - 90° - 30° = 60°
Следствия из теоремы
- Оба острых угла в сумме дают 90°
- Если один острый угол известен, второй можно найти вычитанием из 90°
- В равнобедренном прямоугольном треугольнике острые углы равны по 45°
Применение на практике
| Область | Пример использования |
| Строительство | Расчет углов кровли, лестниц |
| Навигация | Определение курса по треугольнику скоростей |
| Астрономия | Вычисление параллакса небесных тел |
Знание о сумме углов прямоугольного треугольника является фундаментальным для решения множества геометрических задач и находит широкое применение в различных областях человеческой деятельности.