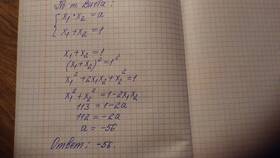В алгебре сумма корней уравнения связана с его коэффициентами определенными математическими зависимостями. В данной статье рассмотрим, как найти сумму корней для различных типов уравнений.
Содержание
Квадратные уравнения
Для квадратного уравнения вида ax² + bx + c = 0 сумма корней определяется по теореме Виета:
| Уравнение | Сумма корней (x₁ + x₂) |
| ax² + bx + c = 0 | -b/a |
Пример
Для уравнения 2x² - 5x + 3 = 0:
- a = 2, b = -5
- x₁ + x₂ = -(-5)/2 = 2.5
Кубические уравнения
Для уравнения вида ax³ + bx² + cx + d = 0 сумма корней равна:
| Уравнение | Сумма корней (x₁ + x₂ + x₃) |
| ax³ + bx² + cx + d = 0 | -b/a |
Уравнения n-ной степени
Для общего полиномиального уравнения:
| Уравнение | Сумма корней |
| aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀ = 0 | -aₙ₋₁/aₙ |
Особые случаи
- Если уравнение имеет один корень кратности n, сумма равна n*x₁
- Для комплексных корней сумма включает все корни с учетом их кратности
Практическое применение
- Проверка правильности найденных корней
- Определение коэффициентов уравнения по известным корням
- Упрощение решения систем уравнений
Ограничения
Теорема Виета и ее обобщения работают только для уравнений с хотя бы одним корнем. Для уравнений без действительных корней в действительных числах сумма не определена.
Заключение
Сумма корней уравнения связана с его коэффициентами простыми соотношениями, которые позволяют находить эту характеристику без непосредственного решения уравнения. Эти зависимости широко применяются в алгебре и математическом анализе.